R software for robust geostatistical modelling of soil survey and monitoring data
Most of geostatistical software, available either commercially in GIS or in statistical software packages or as open source software (e.g. in R, cf. external page www.r-project.org) rely on non-robust algorithms. This is unfortunate, because outlying observations are rather the rule than the exception in environmental data sets. Outlying observations may results from errors (e.g. in data transcription) or from local perturbations in the processes that are responsible for a given pattern of spatial variation. As an example, the spatial distribution of some trace metal in the soils of a region may be distorted by emissions of local anthropogenic sources. Outliers affect the modelling of the large-scale spatial variation (trend), the estimation of the spatial dependence of the residual variation and the predictions by kriging. Identifying outliers manually is cumbersome and requires expertise. A better approach is to use robust algorithms that prevent automatically that outlying observation have undue influence. However, much of the robust statistical methods were developed for independent data. The only notable exception is the robust estimation of the variogram which has found considerable attention in recent geostatistical studies.
In this project we develop a novel method for robust restricted maximum likelihood (REML) estimation of the variogram of a Gaussian random field that is possibly contaminated by independent errors from a long-tailed distribution. Besides robust estimates of the drift and variogram parameters, the method also provides robustified kriging predictions. Unlike the case of Gaussian errors the restricted likelihood function cannot be evaluated easily for a Huber-type long-tailed error distribution. We therefore use Laplace approximations to obtain a closed-form expression fo the restricted log-likelihood that we maximize numerically with respect to the covariance parameters. As by-product we obtain also robust external drift kriging predictions. We studied the robustness properties of the proposed method on simulated contaminated Gaussian random fields, using customary diagnostics for robust statistics (sensitivity curves, bias and variance in replicated simulations). Furthermore, we tested the method with environmental data sets.

Figure 1: Simulated Gaussian data along a transect where the datum at position s = 0.895 is turned into an outlier by adding a contamination of varying magnitude. A range of outlying values is represented by the coloured dots.
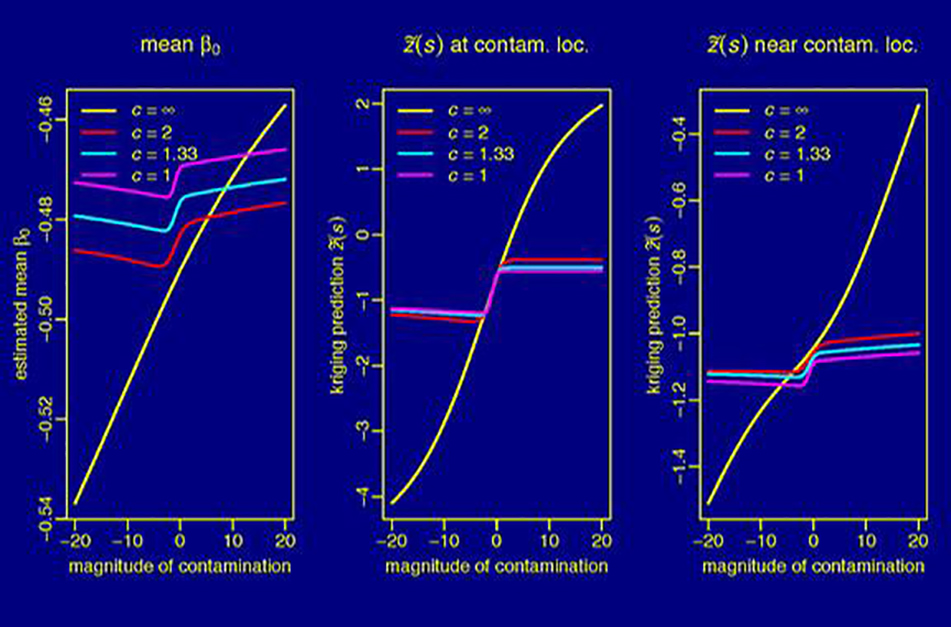
Figure 2: Changes of the estimated mean parameter of the Gaussian process (left), of the predicted (uncontaminated) datum at the contamination location s = 0.895 (middle) and of the predicted datum at s = 0.905 as a function of the magnitude of the contamination and of the tuning parameter c, which controls the robustness of the procedure. In the non-robust case (c=∞) the mean and the predictions change unboundedly with the magnitude of the contamination, in the robust case (small c values) the estimate of the mean and the predictions are less sensitive to the contamination but not strictly bounded.
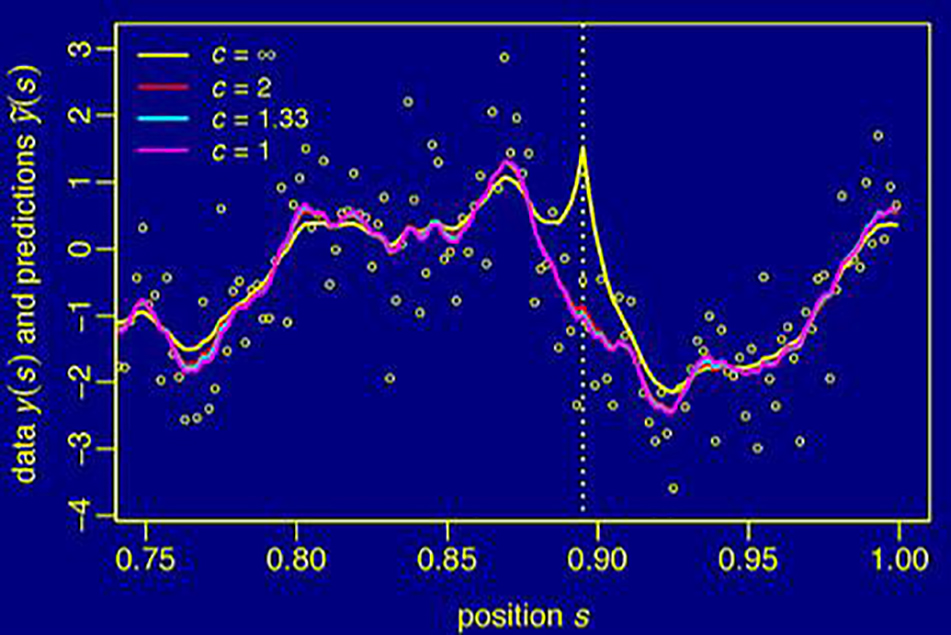
Figure 3: Simulated data in right part of the transect shown in Fig. 1 with predicted values for a contamination of +20 at the location s=0.895 for different values of the robustness tuning parameter c. Unlike the robust predictions (c≤2) the non-robust predictions (c=∞) are severely affected by the outlier.
The developed algorithms are implemented in R and will be bundled as an add-on package. Its use will be illustrated by case studies. To this aim, we shall analyse data available from the National Soil Database (NABODAT) that is currently set-up under the auspices of the Swiss National Soil Monitoring Network (NABO) and the Federal Office for the Environment. Using the developed software, the case studies will present some step-by-step robust geostatistical analyses of soil data, which should demonstrate to potential users of our software the benefit of robust geostatistical analyses of soil data.
Team: Andreas Papritz, Cornelia Schwierz, Armin Keller (Swiss Soil Monitoring Network, NABO), Kirsten Rehbein (NABO) in collaboration with Hans R. Kuensch & Werner A. Stahel (Seminar for Statistics, ETH Zurich)
Funding: Swiss Federal Office for the Environment FOEN
Contact: